A particularity of the Poisson distribution is that the convolution of m such distributions with parameters a1, ..., am is again a Poisson distribution with parameter a = a1+a2+...+am, and it is the only distribution with this convenient property.
http://www.absoluteastronomy.com/encyclopedia/P/Po/Poisson_process.htm
The number of telephone calls arriving at a switchboard during any specified time interval may have a Poisson distribution, and the number of calls arriving during one time interval may be
statistically independent of the number of calls arriving during any other non-overlapping time interval. This is a one-dimensional Poisson process. In simple models, one may assume a constant average rate of arrival, e.g., λ = 12.3 calls per minute. In that case, the
expected value of the number of calls in any time interval is that rate times the amount of time, λ
t. In messier and more realistic problems, one uses a non-constant rate function λ(
t). In that case, the expected value of the number of calls between time
a and time
b is

The number of bombs falling on a specified area of London in the early days of the Second World War may be a random variable with a Poisson distribution, and the number of bombs falling on two areas of the city that do not overlap may be statistically independent. This is a 2-dimensional Poisson process.

Astonomers may treat the number of stars in a given volume of space as a random variable with a Poisson distribution, and the numbers of stars in any two or more non-overlapping regions as statistically independent. This is a 3-dimensional Poisson process.


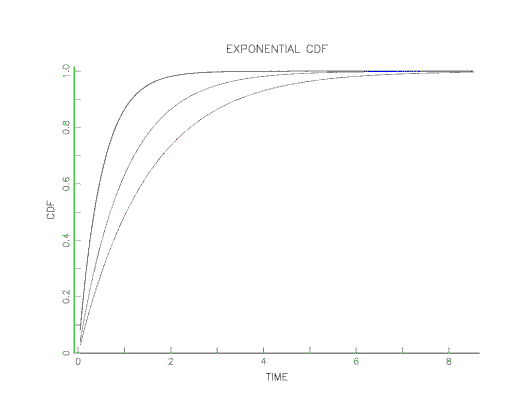
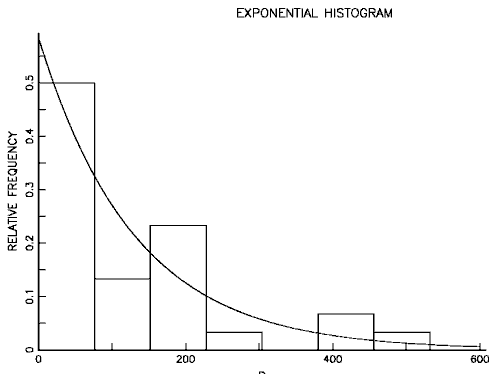
 for any time. The exponential distribution is the only distribution to have a constant failure rate. Also, another name for the exponential mean is the Mean Time To Fail or MTTF and we have MTTF = 1/
for any time. The exponential distribution is the only distribution to have a constant failure rate. Also, another name for the exponential mean is the Mean Time To Fail or MTTF and we have MTTF = 1/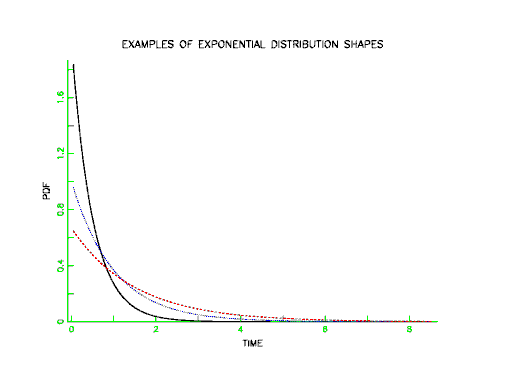


 The number of bombs falling on a specified area of London in the early days of the Second World War may be a random variable with a Poisson distribution, and the number of bombs falling on two areas of the city that do not overlap may be statistically independent. This is a 2-dimensional Poisson process.
The number of bombs falling on a specified area of London in the early days of the Second World War may be a random variable with a Poisson distribution, and the number of bombs falling on two areas of the city that do not overlap may be statistically independent. This is a 2-dimensional Poisson process.